Category: Allgemein

Customizing map background in Tableau

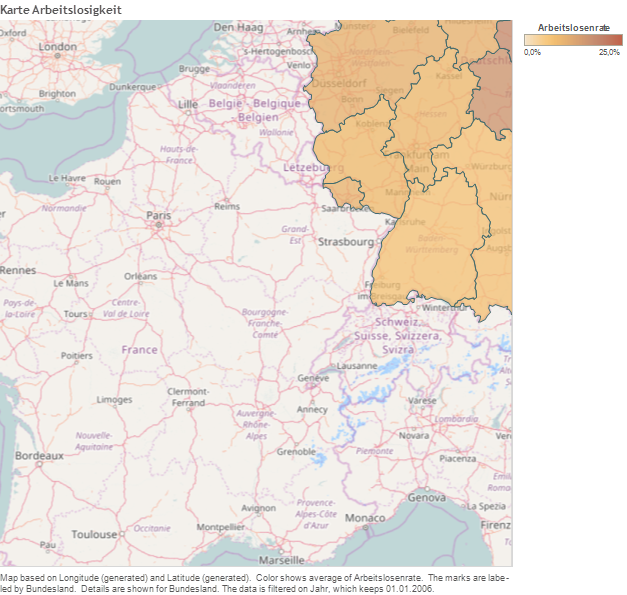
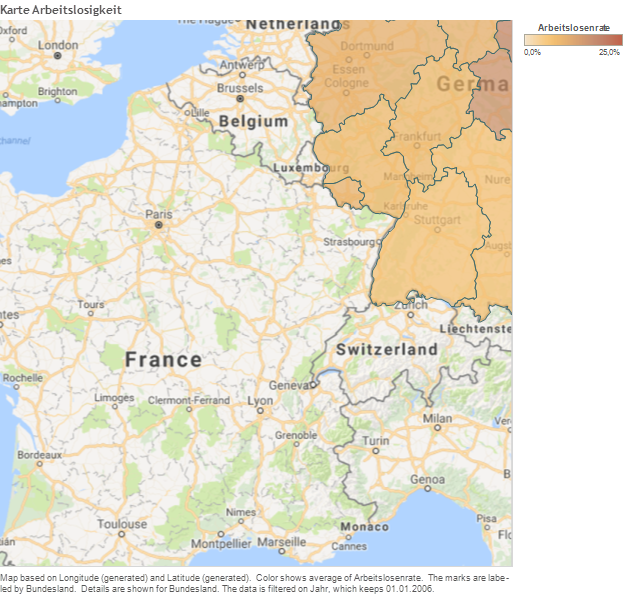
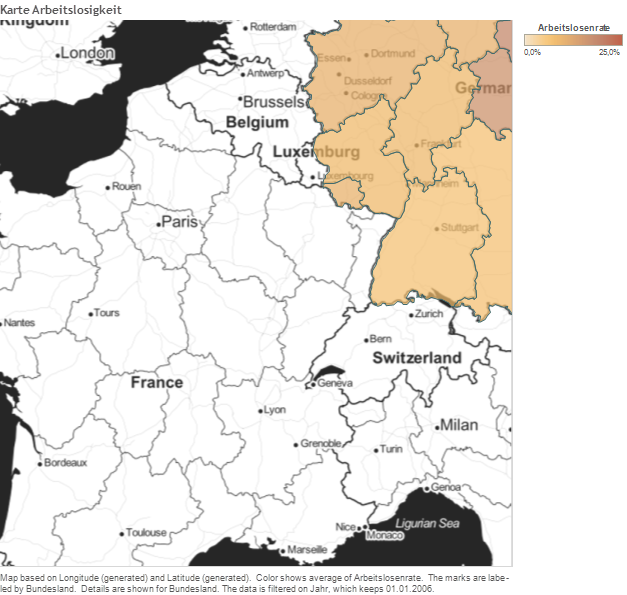
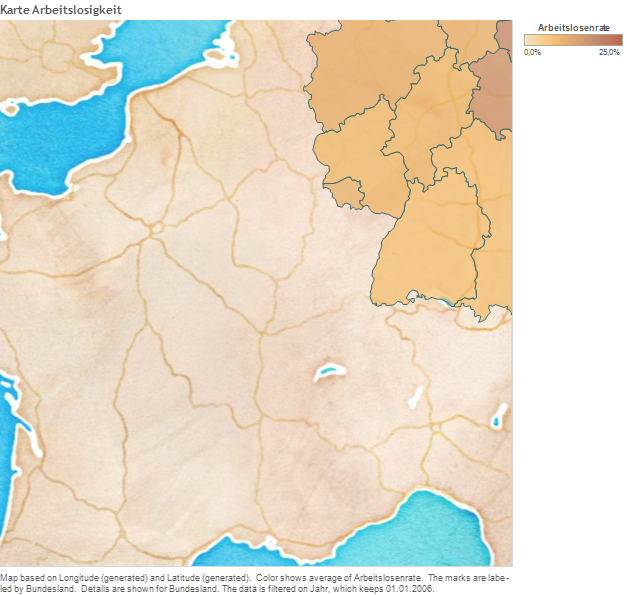
Tableau Desktop includes a connection to Tableau’s map server, which provides an extensive selection of maps optimized for use with Tableau. If you prefer to use your own maps, the easiest approach is to connect to a map server that supports the WMS standard. For more information, go to Working with WMS Servers topic in Tableau Desktop Help and Mapping Data with WMS article.

Requirements for a TMS Connection

To connect to your map server from the TMS, your map server must have the following features:

  • Maps are returned as a collection of tiles
  • Tiles are in Web Mercator projection
  • Tiles can be addressed by URL using the same numbering scheme as common web mapping services. For more information, see the <url-format> section under Variables in the TMS File for more information.

Create a Simple TMS File

To connect to the TMS, you must create a TMS file. A TMS file is a simple text file that you can create in a text editor.

Open a text editor.Copy and paste the following XML into the text editor.

Copy and paste the following XML into the text editor.<?xml version="1.0" encoding="utf-8"?>
<mapsource inline="<boolean>" version="8.1">
<connection class="OpenStreetMap" port="80" server="<server-url>" url-format="<url-format>" />
<layers>
<layer display-name='Base' name='base' show-ui='false' type='features' request-string='/' />
</layers>
</mapsource>

Replace <boolean>, <server-url>, and <url-format> variables as described in the Required Variables in the TMS File section in this article.

Save the TMS file with a .tms extension to the Mapsources folder of Tableau Desktop or Tableau Server.The default location for the Mapsources folder:

For Tableau Desktop on the Mac – /Users/<user>/Documents/My Tableau Repository/Mapsources

For Tableau Desktop on Windows – C:\Users\<user>\Documents\My Tableau Repository\Mapsources

For Tableau Server – C:\Program Files\Tableau\Tableau Server\<version>\vizqlserver\mapsources

Open Tableau Desktop.

Connect to a workbook that contains location information.

Select Map > Background Maps, and then select the background map from the map server you configured in the TMS file.

(Optional) If you added the TMS file to the Mapsources folder in Tableau Server, publish the workbook to Tableau Server and see the background map you configured in the TMS file.

Required Variables in the TMS File

Only the following variables can be changed in the XML:

<boolean>: Replace the <boolean> with either a true or false value.

A true value allows Tableau Desktop to save the configuration specified in the TMS file with the workbook. Use this value if your workbook is being published to Tableau Online or Tableau Public.

A false value requires Tableau Desktop or Tableau Server to have access to the TMS file saved in the Mapsources folder to display the maps from your map server.

<server-url>: Replace <server-url> with the URL of your map server.

<url-format>: Replace <url-format> with additional URL fragments that your map server requires. This might include the following tags:

{Z}: The {Z} tag indicates the zoom level. A zoom level of 0 displays the entire world in one map tile. The TMS will fetch map tiles up to level 16.

{X} and {Y}: The {X} and {Y} tags indicate the map tile coordinates. For more information about map tiles, refer to the following web pages:

OpenStreetMaps wiki page

Bing Maps web page

OSM XML

Suppose you want to connect to a sample map server provided by OpenStreetMaps. The TMS file may look like the following:

<?xml version="1.0" encoding="utf-8"?>
<mapsource inline="true" version="8.1">
<connection class="OpenStreetMap" port="80" server="http://a.tile.openstreetmap.org" url-format="/{Z}/{X}/{Y}.png" />
<layers>
<layer display-name='Base' name='base' show-ui='false' type='features' request-string='/' />
</layers>
</mapsource>

Google maps XML

The TMS file for the google map tile server looks like the following:

<?xml version="1.0" encoding="utf-8"?>
<mapsource inline="true" version="8.1">
<connection class="OpenStreetMap" port="80" <connection class="OpenStreetMap" port="80" server="http://mt1.google.com" url-format="/vt/lyrs=m&amp;x={X}&amp;y={Y}&amp;z={Z}" />
<layers>
<layer display-name='Base' name='base' show-ui='false' type='features' request-string='/' />
</layers>
</mapsource>

Stamen Toner XML

Suppose you want to connect to a sample map server provided by OpenStreetMaps. The TMS file may look like the following:

<?xml version="1.0" encoding="utf-8"?>
<mapsource inline="true" version="8.1">
<connection class="OpenStreetMap" port="80" <connection class="OpenStreetMap" port="80"
server="http://tile.stamen.com" url-format="/toner/{Z}/{X}/{Y}.png" />
<layers>
<layer display-name='Base' name='base' show-ui='false' type='features' request-string='/' />
</layers>
</mapsource>

Stamen WaterColor XML

Suppose you want to connect to a sample map server provided by OpenStreetMaps. The TMS file may look like the following:

<?xml version="1.0" encoding="utf-8"?>
<mapsource inline="true" version="8.1">
<connection class="OpenStreetMap" port="80" <connection class="OpenStreetMap" port="80"
<connection class="OpenStreetMap" port="80" server="http://tile.stamen.com" url-format="/watercolor/{Z}/{X}/{Y}.jpg" />
<layers>
<layer display-name='Base' name='base' show-ui='false' type='features' request-string='/' />
</layers>
</mapsource>

 

Offline maps: local map tile server

As described previously (e.g. http://rgooglemaps.r-forge.r-project.org/OfflineMaps-RgoogleMaps-leaflets.html) we can use the RgoogleMaps package to (i) download map tiles and store them locally and (ii) launch a local Web server (in python or in R) to serve the map tiles to ANY mapping application.

To achieve this in Tableau, you would simply follow the instructions from the link above and then use e.g. this XML file:

<?xml version="1.0" encoding="utf-8"?>
<mapsource inline="true" version="8.1">
<connection class="OpenStreetMap" port="80" <connection class="OpenStreetMap" port="80"
<connection class="OpenStreetMap" port="80" server="http:/localhost:8000" url-format="/mapTiles/watercolor/{Z}/{X}/{Y}.jpg" />
<layers>
<layer display-name='Base' name='base' show-ui='false' type='features' request-string='/' />
</layers>
</mapsource>

Alternative to the Hypergeometric Formula

The Hypergeometric Distribution is usually explained via an urn analogy and formulated as the ratio of “favorable outcomes” to all possible outcomes:

\[
\displaystyle
\boxed{P(x=a;N,A,n,a) = \frac{{A \choose a} \cdot {N-A \choose n-a} }{{N \choose n}}}
\]

where \(N\) is the total number of balls in, \(A\) the number of “red” balls in the urn, and \(n\) the sample size. The question answered by the above expression is the probability of finding \(x=a\) red balls in the sample.

However, a different – equally worthy – viewpoint is that of a tree with conditional probabilities.

Here is an example for \(N=10, A=4, n=3\)

So there are 3 leafs with exactly one red ball in the sample. Following the tree we multiply the conditional probabilities of the tree egdes to get to the “and” probability of the leafs. It should be clear that all three probabilites are identical – but for the order of multiplication:

\[
P (\mbox{one red}) = 3 \cdot P_{leaf} = 3 \cdot \frac{4}{10} \cdot \frac{6}{9} \cdot \frac{5}{8} = 3 \cdot \frac{4 \cdot 6 \cdot 5}{10 \cdot 9 \cdot 8}
\]

Alternative formula

How many leafs contain exactly one red ball? Exactly \({n \choose a} = {3 \choose 1} = 3\). The probability for the precise event “a red balls followed by n-a blue balls”is:

\[
\frac{A}{N} \cdot \frac{A-1}{N-1} \cdots \frac{A-a+1}{N-a+1} \cdot \frac{N-A}{N-a} \cdot \frac{N-A-1}{N-a-1} \cdots \frac{N-A-(n-a-1)}{N-a-(n-a-1)}
\] The last denominator is simply \(N-n+1\), i.e. the full denominator is \(_NV_n=N!/(N-n)!\)

The left numerator is simply \(_AV_n = A!/(A-a)!\) in analogy the right numerator \(_{N-A}V_{n-a} = (N-A)!/(N-A-(n-a))!\) So, all in all \[
{n \choose a} \cdot \frac{_AV_n \cdot _{N-A}V_{n-a}}{_NV_n} = {n \choose a} \cdot \frac{A! \cdot (N-A)! \cdot (N-n)!}{(A-a)! \cdot (N-A-(n-a))! \cdot N!}
\]

\[
= {n \choose a} \cdot \frac{\frac{A!}{(A-a)!} \cdot \frac{(N-A)!}{(N-A-(n-a))!} }{\frac{N!}{(N-n)!}} = \frac{{A \choose a} \cdot {N-A \choose n-a} }{{N \choose n}}
\]

which leaves us with \[
\displaystyle
\boxed{P(x=a;N,A,n,a) = {n \choose a} \cdot \frac{_AV_n \cdot _{N-A}V_{n-a}}{_NV_n} }
\]