Variable Importance in Random Forests can suffer from severe overfitting
Predictive vs. interpretational overfitting
There appears to be broad consenus that random forests rarely suffer from “overfitting” which plagues many other models. (We define overfitting as choosing a model flexibility which is too high for the data generating process at hand resulting in non-optimal performance on an independent test set.) By averaging many (hundreds) of separately grown deep trees -each of which inevitably overfits the data – one often achieves a favorable balance in the bias variance tradeoff.
For similar reasons, the need for careful parameter tuning also seems less essential than in other models.
This post does not attempt to contribute to this long standing discussion (see e.g. https://stats.stackexchange.com/questions/66543/random-forest-is-overfitting) but points out that random forests’ immunity to overfitting is restricted to the predictions only and not to the default variable importance measure!
We assume the reader is familiar with the basic construction of random forests which are averages of large numbers of individually grown regression/classification trees. The random nature stems from both “row and column subsampling’’: each tree is based on a random subset of the observations, and each split is based on a random subset of candidate variables. The tuning parameter – which for popular software implementations has the default \(\lfloor p/3 \rfloor\) for regression and \(\sqrt{p}\) for classification trees – can have profound effects on prediction quality as well as the variable importance measures outlined below.
At the heart of the random forest library is the CART algorithm which chooses the split for each node such that maximum reduction in overall node impurity is achieved. Due to the CART bootstrap row sampling, \(36.8\%\) of the observations are (on average) not used for an individual tree; those “out of bag” (OOB) samples can serve as a validation set to estimate the test error, e.g.:
\[\begin{equation}
E\left( Y – \hat{Y}\right)^2 \approx OOB_{MSE} = \frac{1}{n} \sum_{i=1}^n{\left( y_i – \overline{\hat{y}}_{i, OOB}\right)^2}
\end{equation}\]
where \(\overline{\hat{y}}_{i, OOB}\) is the average prediction for the \(i\)th observation from those trees for which this observation was OOB.
Variable Importance
The default method to compute variable importance is the mean decrease in impurity (or gini importance) mechanism: At each split in each tree, the improvement in the split-criterion is the importance measure attributed to the splitting variable, and is accumulated over all the trees in the forest separately for each variable. Note that this measure is quite like the \(R^2\) in regression on the training set.
The widely used alternative as a measure of variable importance or short permutation importance is defined as follows:
\[\begin{equation}
\label{eq:VI}
\mbox{VI} = OOB_{MSE, perm} – OOB_{MSE}
\end{equation}\]
(more pointers in https://stackoverflow.com/questions/15810339/how-are-feature-importances-in-randomforestclassifier-determined)
Gini importance can be highly misleading
We use the well known titanic data set to illustrate the perils of putting too much faith into the Gini importance which is based entirely on training data – not on OOB samples – and makes no attempt to discount impurity decreases in deep trees that are pretty much frivolous and will not survive in a validation set.
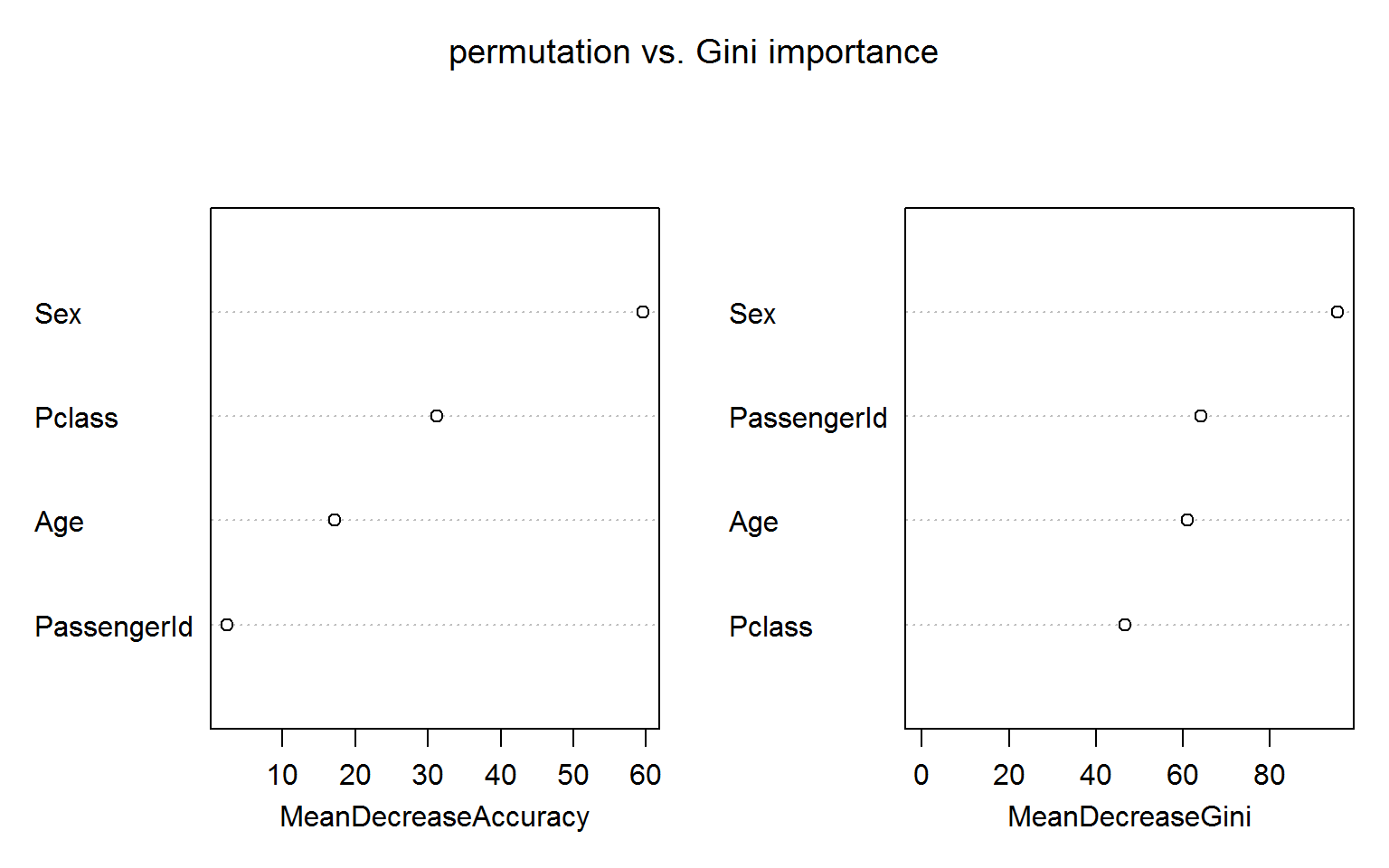
In the following model we include passengerID as a feature along with the more reasonable Age, Sex and Pclass: randomForest(Survived ~ Age + Sex + Pclass + PassengerId, data=titanic_train[!naRows,], ntree=200,importance=TRUE,mtry=2)
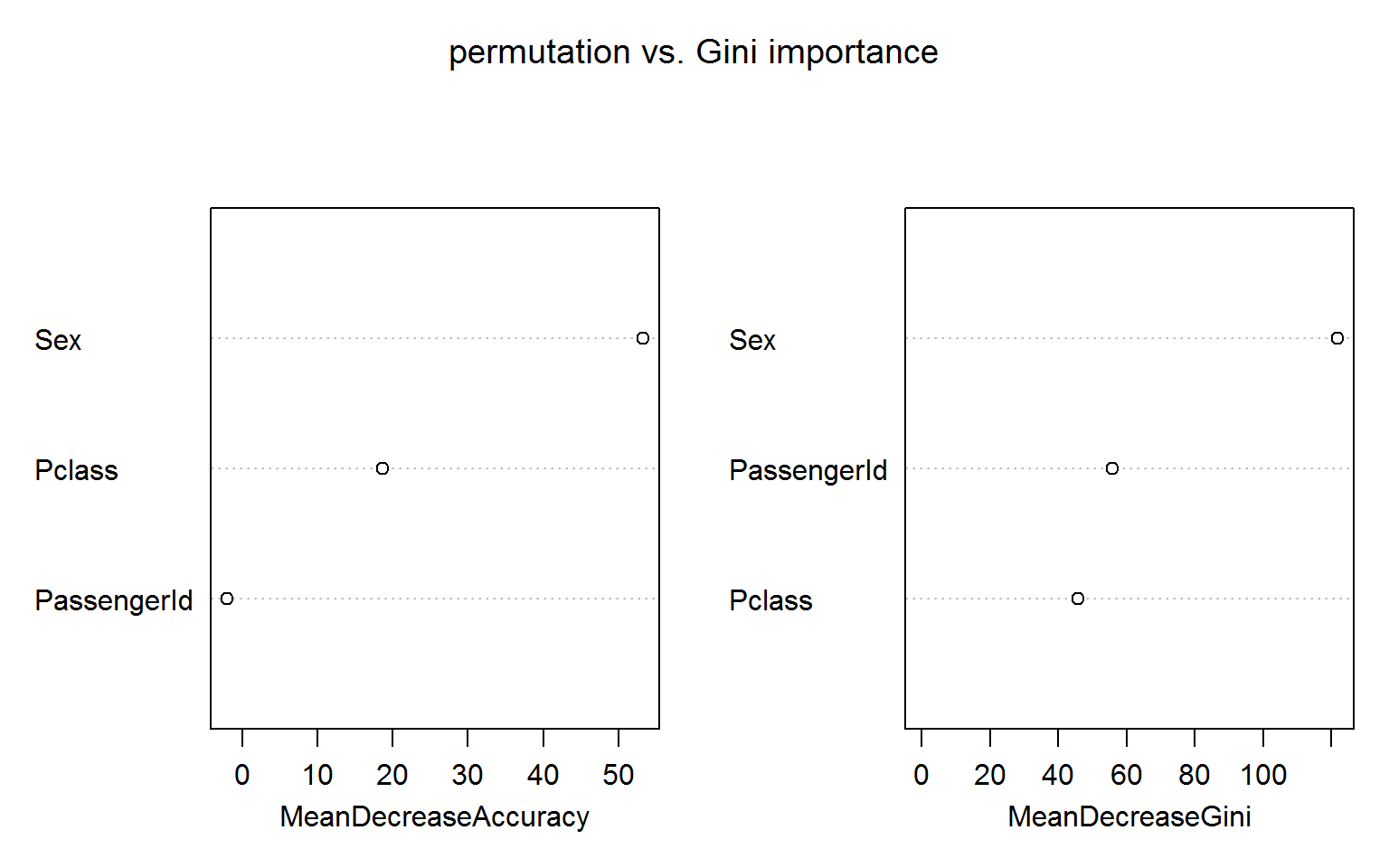
The figure below shows both measures of variable importance and surprisingly passengerID turns out to be ranked number 2 for the Gini importance (right panel). This unexpected result is robust to random shuffling of the ID.
The permutation based importance (left panel) is not fooled by the irrelevant ID feature. This is maybe not unexpected as the IDs shold bear no predictive power for the out-of-bag samples.
Noise Feature
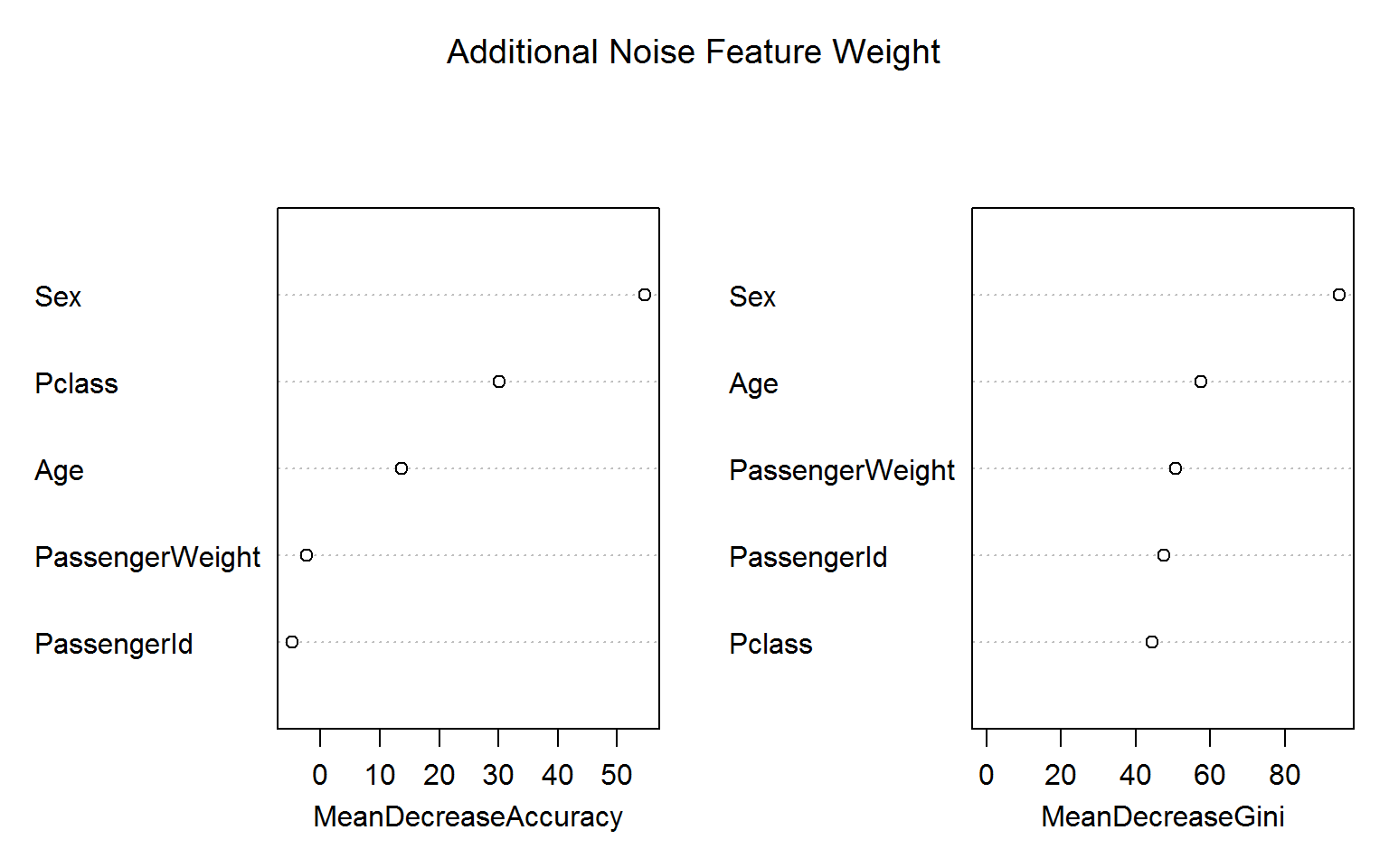
Let us go one step further and add a Gaussian noise feature, which we call PassengerWeight:
titanic_train$PassengerWeight = rnorm(nrow(titanic_train),70,20)
rf4 =randomForest(Survived ~ Age + Sex + Pclass + PassengerId + PassengerWeight, data=titanic_train[!naRows,], ntree=200,importance=TRUE,mtry=2)Again, the blatant “overfitting” of the Gini variable importance is troubling whereas the permutation based importance (left panel) is not fooled by the irrelevant features. (Encouragingly, the importance measures for ID and weight are even negative!)
In the remainder we investigate if other libraries suffer from similar spurious variable importance measures.
h2o library
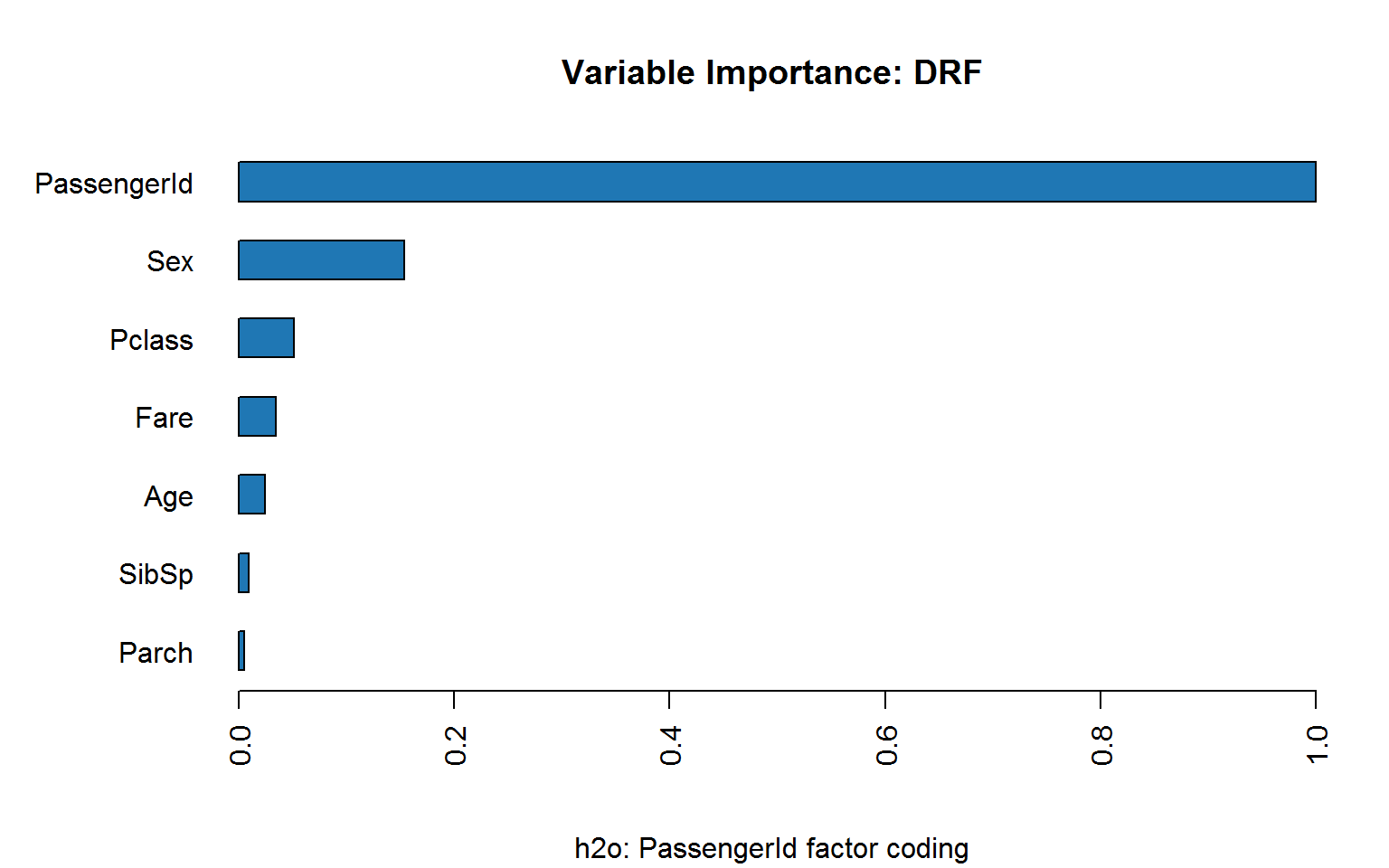
Unfortunately, the h2o random forest implementation does not offer permutation importance:
Coding passenger ID as integer is bad enough:
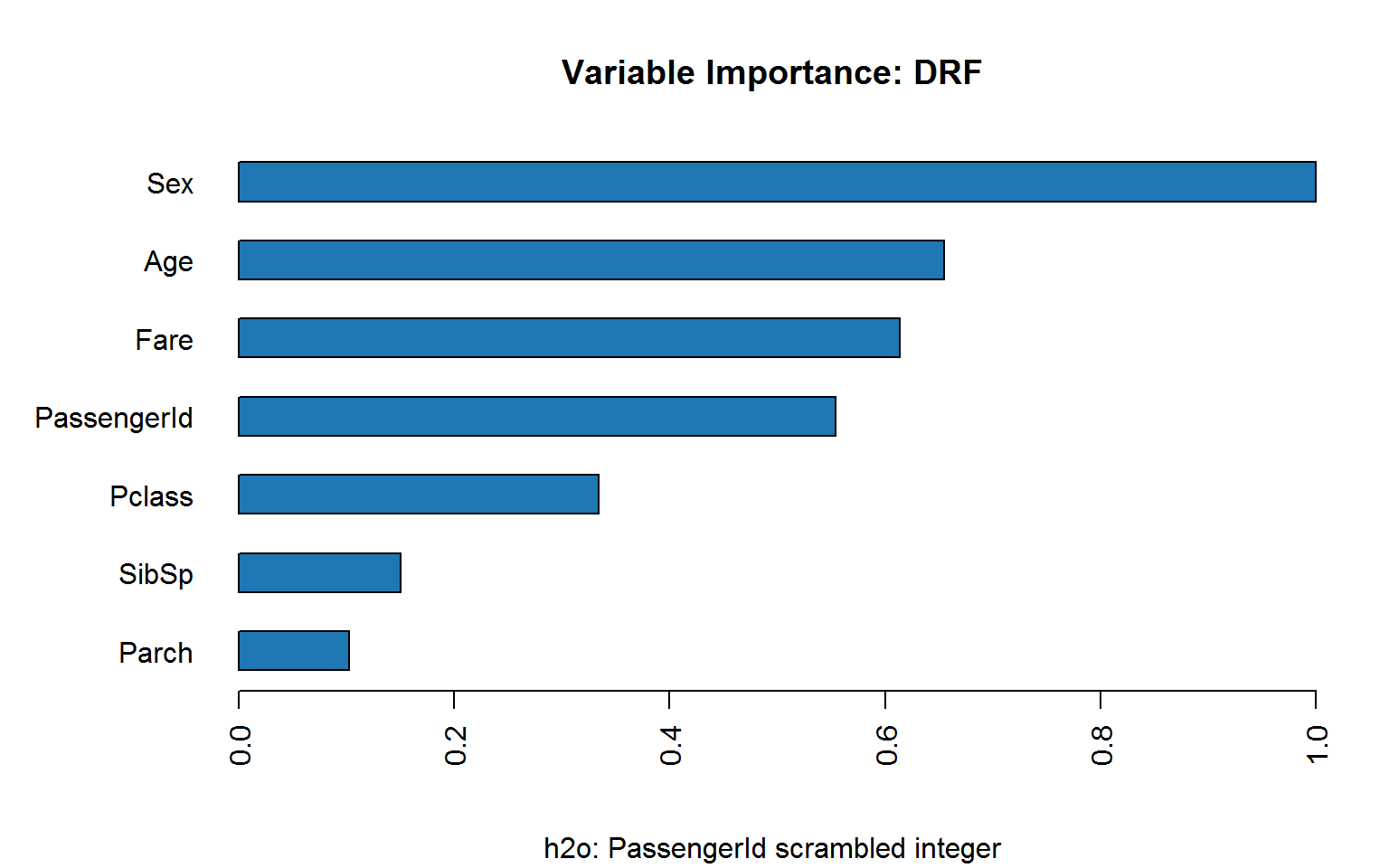
Coding passenger ID as factor makes matters worse:
Let’s look at a single tree from the forest:
If we scramble ID, does it hold up?
partykit
conditional inference trees are not being fooled by ID:
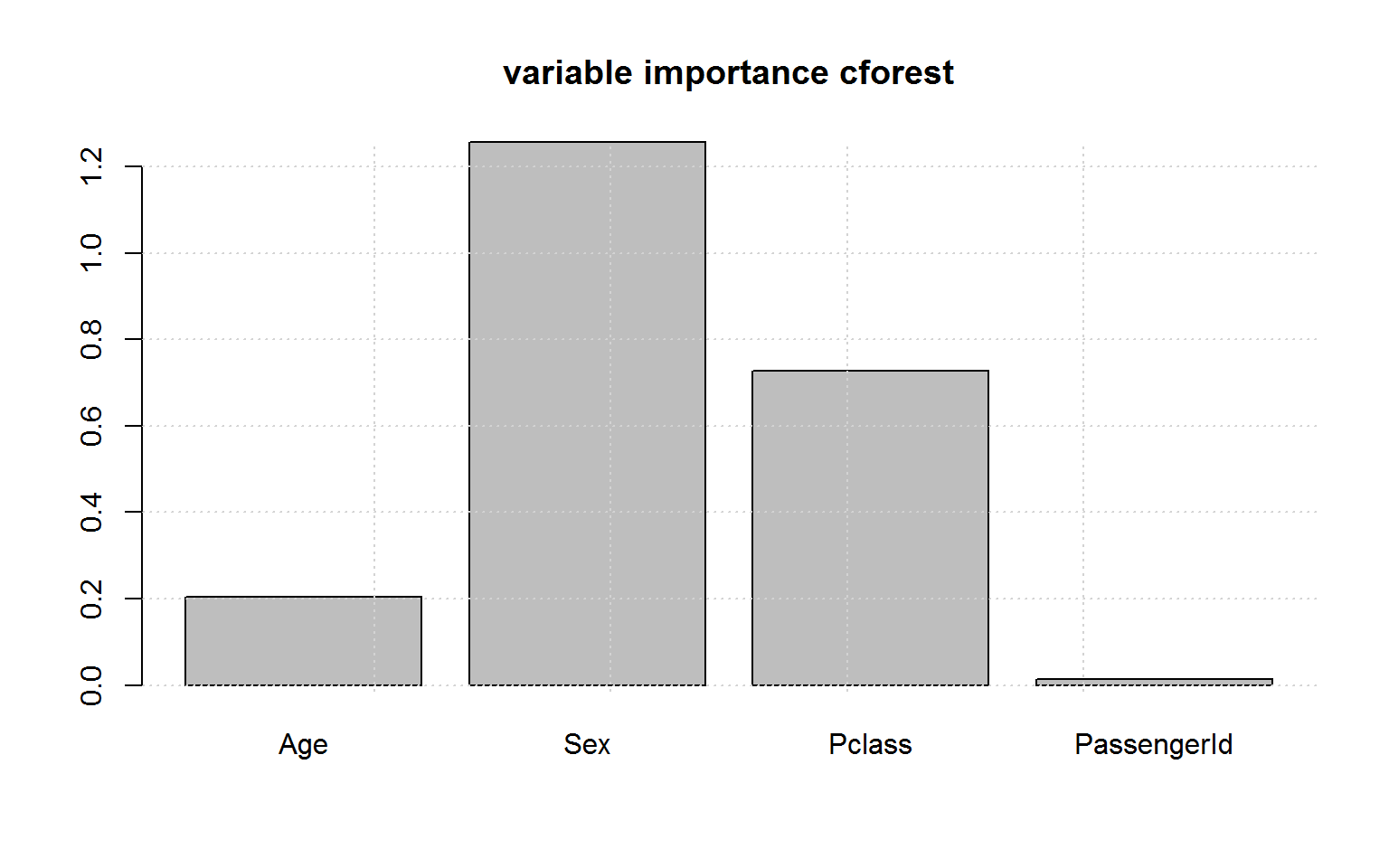
And the variable importance in cforest is indeed unbiased
python’s sklearn
Unfortunately, like h2o the python random forest implementation offers only Gini importance, but this insightful post offers a solution:
Gradient Boosting
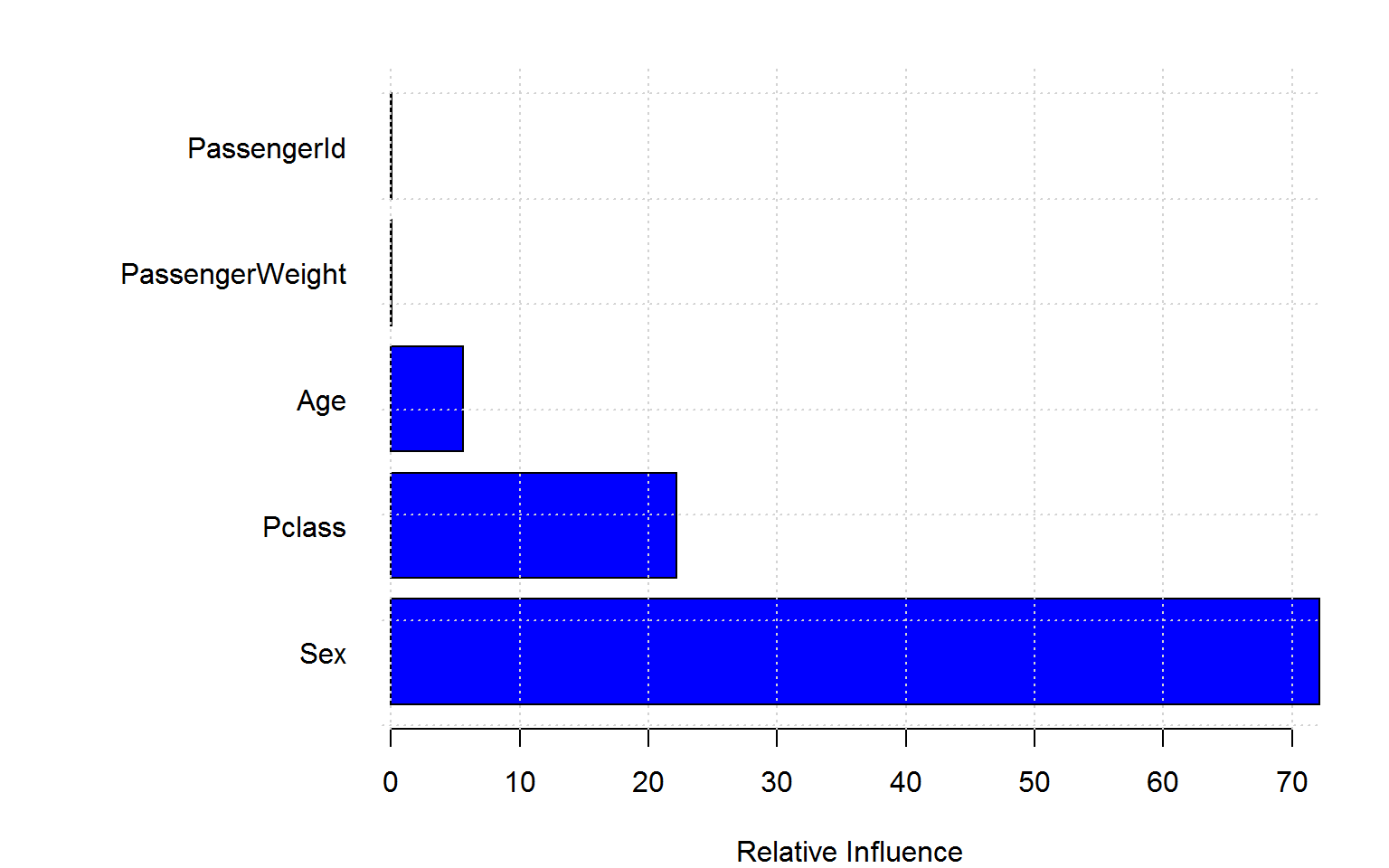
Boosting is highly robust against frivolous columns:
mdlGBM = gbm(Survived ~ Age + Sex + Pclass + PassengerId +PassengerWeight, data= titanic_train, n.trees = 300, shrinkage = 0.01, distribution = "gaussian")Conclusion
Sadly, this post is 12 years behind:
It has been known for while now that the Gini importance tends to inflate the importance of continuous or high-cardinality categorical variables:
the variable importance measures of Breiman’s original Random Forest method … are not reliable in situations where potential predictor variables vary in their scale of measurement or their number of categories.
(Strobl et al, 2007 Bias in random forest variable importance measures: Illustrations, sources and a solution)
Single Trees
I am still struggling with the extent of the overfitting. It is hard to believe that passenger ID could be chosen as a split point early in the tree building process given the other informative variables! Let us inspect a single tree
## rowname left daughter right daughter split var split point status
## 1 1 2 3 Pclass 2.5 1
## 2 2 4 5 Pclass 1.5 1
## 3 3 6 7 PassengerId 10.0 1
## 4 4 8 9 Sex 1.5 1
## 5 5 10 11 Sex 1.5 1
## 6 6 12 13 PassengerId 2.5 1
## prediction
## 1 <NA>
## 2 <NA>
## 3 <NA>
## 4 <NA>
## 5 <NA>
## 6 <NA>This tree splits on passenger ID at the second level !! Let us dig deeper:
The help page states
For numerical predictors, data with values of the variable less than or equal to the splitting point go to the left daughter node.
So we have the 3rd class passengers on the right branch. Compare subsequent splits on (i) sex, (ii) Pclass and (iii) passengerID:
Starting with a parent node Gini impurity of 0.184
Splitting on sex yields a Gini impurity of 0.159
| 1 | 2 | |
|---|---|---|
| 0 | 72 | 303 |
| 1 | 71 | 50 |
Splitting on passengerID yields a Gini impurity of 0.183
| FALSE | TRUE | |
|---|---|---|
| 0 | 2 | 373 |
| 1 | 3 | 118 |
And how could passenger ID accrue more importance than sex ?